Reinforcement learning (RL) algorithms are known to be brittle to the choice of hyperparameters (1). Thus, the case for automating the discovery of RL hyperparameters is clear:

• To make the algorithms generalize to new environments, we need a way to find configurations for an arbitrary task. 

• To make the field accessible to those without vast resources, we need our approach to be as efficient as possible.

• For those with the capacity to scale, AutoRL algorithms can potentially achieve significantly better results. Most notably, AlphaGo used Bayesian Optimization to improve performance before the final match, and we all know how that ended.

In our most recent paper recently published at NeurIPS 2020, we introduce a new method for training neural networks: Population-Based Bandits (PB2). 

Similar to Population Based Training (PBT), PB2 trains and optimizes a series of networks at the same time, allowing the optimal set-up to be quickly found. However, unlike PBT, PB2 uses a probabilistic model to guide the search in an efficient way, making it possible to discover high performing hyperparameter configurations with far fewer agents than typically required by prior work.

We recently open sourced PB2 as a new algorithm in Ray Tune v1.0.1 so you can try it out yourself! You can check out the documentation, and also try out our full example leveraging PB2 for reinforcement learning.

LinkWhat are the main methods for hyperparameter optimization?

To provide context for PB2, let’s quickly overview some of the most popular methods for hyperparameter optimization.

LinkRandom Search & Grid Search

Two of the most basic hyperparameter tuning strategies are parallel random search and grid search. Typically, random search/grid search is specified by a search space, which can be a distribution (like a multivariate uniform or normal distribution), or a enumerated list of values (in the case of grid search).

Random search and grid search are the most common hyperparameter optimization techniques. They are quick to run as they are easily parallelizable but are highly inefficient as they do not use any information across the trials.

LinkBayesian optimization

A more efficient approach for hyperparameter optimization is  Bayesian Optimization. Bayesian optimization aims to minimize the number of evaluations (or hyperparameters tried) while maximizing the performance of the model by fitting a Gaussian model to predict model performance in order to inform future hyperparameters. 

Bayesian optimization is inherently sequential (as seen in the figure), as it relies on prior information to make new decisions/consider which hyperparameters to try next. As a result, it often takes longer to run in wallclock time but is more efficient due to using information from all trials.

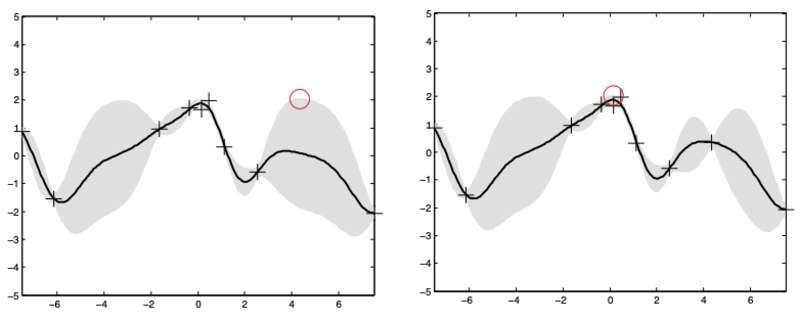Here we see the posterior mean (black line) and standard deviation (grey) of a Gaussian Process. We want to select the next point using an upper confidence bound (UCB), to trade off exploration and exploitation. On the left we first choose the point with high uncertainty, but once we have observed this point, the model’s uncertainty is reduced and we now select the next point based on high expected value. This figure is taken from the GP-UCB paper.

LinkPopulation-based Training

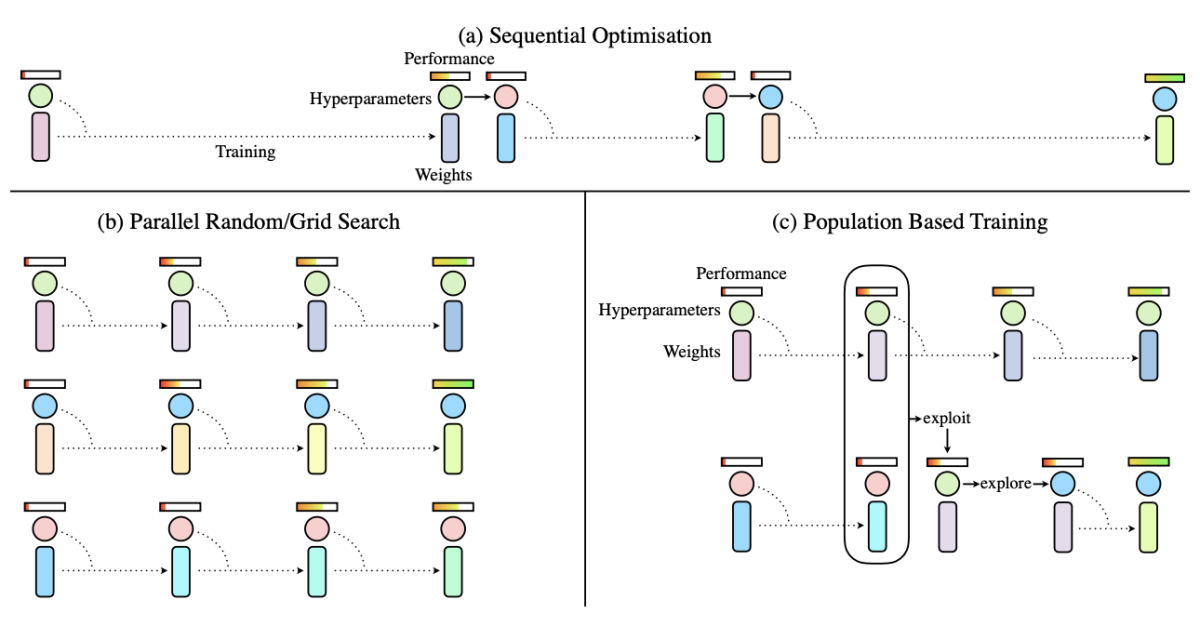Three distinct approaches for hyperparameter tuning. The rectangles correspond to the model weights, while the circles represent hyperparameters. Notice the hyperparameters do not change during a trial for a) or b), but in c) they are adapted in an online fashion. The bars above correspond to performance. This figure is taken from the original PBT paper.

The Population Based Training (PBT) algorithm tries to combine the best of both worlds from Grid/Random search and Bayesian Optimization. It runs trials in parallel but adapts the hyperparameters according to performance of the different agents. 

PBT acts like a human watching their experiments, periodically replacing weaker agents with close copies of better ones. This has been particularly successful in RL, and has been used in a variety of prominent papers in the field.

However, PBT has some drawbacks. Most notably, it relies on a large population to explore the hyperparameter space. When this isn’t present, it can underperform a random baseline.

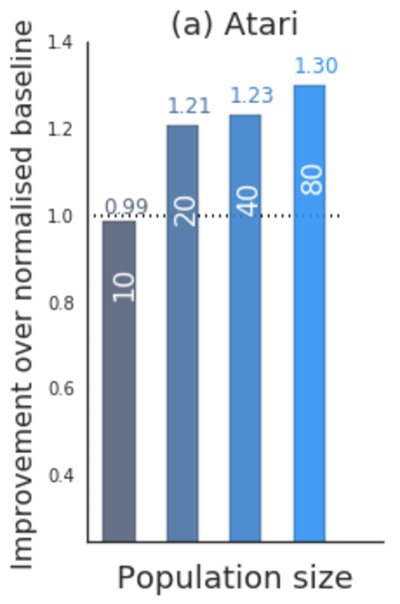In PBT, population can significantly improve performance. Under low population size (parallel trials), performance can actually degrade from baseline. This figure is taken from the original PBT paper.

For a deeper dive on hyperparameters, check out our three-part series on hyperparameter tuning.

LinkPopulation-based Bandits

Using ideas from the GP-bandit optimization literature, PB2 is our new technique for optimizing neural networks based off of PBT. PB2 leverages a Gaussian Process (GP) (probabilistic model) to adapt its model hyperparameters during training.

There are two key differences between PBT and PB2. 

The first is that PB2 uses information from all completed trials to make an informed decision given the success and failure of all historical trials. 

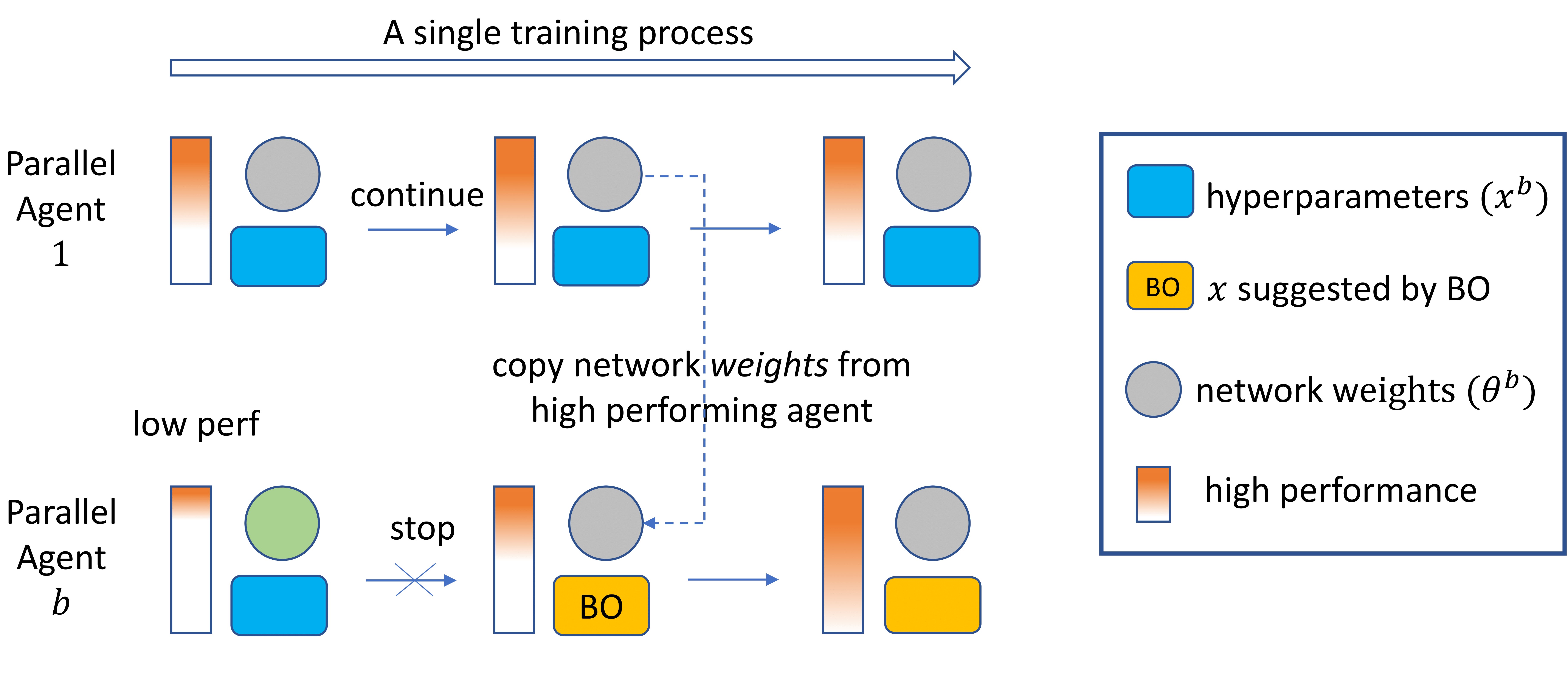After copying the weights from a high performing agent, PB2 uses Bayesian Optimization to retrieve a suggestion based on past trial performance for new hyperparameter values.

In addition, PB2 can select a new configuration anywhere in the search space - this is in stark contrast to PBT which must rely on incrementally mutating an existing configuration. When the space of possible configurations is large and the number of trials is small, it is easy to see that this may make it very hard to reach the regions of the hyperparameter space which lead to strong performance.

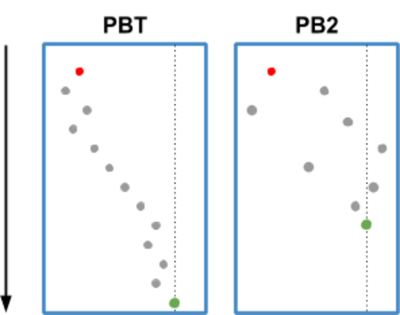Trajectory of a hyperparameter value. The line indicates the optimal value, the red dot is the starting value. In PBT, the parameter has to "crawl" until it reaches the optimal region. In PB2, the parameter can be sampled from the whole training region, potentially reaching it much faster. Additionally, because PB2 models parameter performance, it is likely to sample the parameter in this good region more often.

With this approach, PB2 is theoretically proven to efficiently find good configurations. This is the first such result for a population-based hyperparameter optimization algorithm. 

LinkSo, does it work?

We trained a PPO agent across multiple seeds on the Bipedal Walker environment from OpenAI Gym to compare PB2 with standard Population Based Training.

PB2 is very effective in constrained resource settings. We see that PB2 can efficiently learn high performing configurations with a population size of just 4 agents. This means you can run the whole population in parallel on a laptop. When scaling to 8 agents, PBT does improve, but still underperforms PB2. 

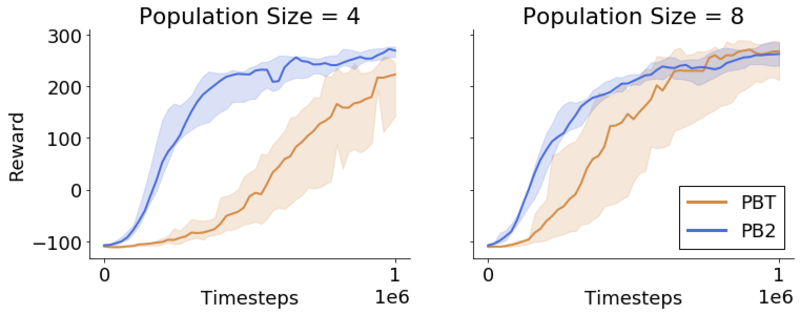The plot shows the median and interquartile range for ten random initializations of both PBT and PB2. On the left we have a population of four agents, and on the right we have eight.

The gifs show what these rewards actually mean. On the left we see the PBT agent with a reward of 220. On the right we see a PB2 agent which gets a reward of 270. It appears to have a much more efficient gait. 

PB2 benefits from its extended range for exploration. As mentioned above, PB2 provides the ability to select a point anywhere inside the hyperparameter range. For example, if we do not know the optimal range, we can set a wide bound and still achieve high performance. 

To test this, we ran the same code again, but increased the range for the batchsize from 1k-60k to 5k-200k. Clearly if we use a batch size of 200k we cannot do too well on the task, this means we can only take five gradient steps! PB2 still performs well, whereas PBT does significantly worse:

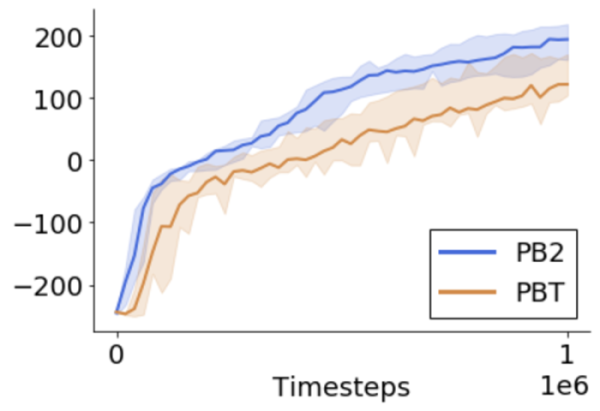The plot shows the median and interquartile range for ten random initializations of both PBT and PB2. In each case, there is a population of four agents.

LinkTry it out yourself

PB2 is included as a new scheduling algorithm in Ray Tune, and is a part of Ray’s 1.0.1 release. You can check out the documentation here:

For the above experiments, you can leverage this code example below, which runs in 30 minutes on a 2019 macbook pro. 

1import ray
2from ray.tune import run, sample_from
3from ray.tune.schedulers.pb2 import PB2
4import random
5
6# Create the PB2 scheduler.
7pb2_scheduler = PB2(
8        time_attr="timesteps_total",
9        metric="episode_reward_mean",
10        mode="max",
11        perturbation_interval=50000,
12        quantile_fraction=0.25,  # copy bottom % with top % (weights)
13        # Specifies the hyperparam search space
14        hyperparam_bounds={
15            "lambda": [0.9, 1.0],
16            "clip_param": [0.1, 0.5],
17            "lr": [1e-3, 1e-5],
18            "train_batch_size": [1000, 60000]
19        })
20
21# Run PPO algorithm experiment on BipedalWalker with PB2.
22analysis = run(
23        "PPO",
24        name="ppo_pb2_bipedal",
25        scheduler=pb2_scheduler,
26        verbose=1,
27        num_samples=4,  # population size
28        stop={"timesteps_total": 1000000},
29        config={
30            "env": "BipedalWalker-v2",
31            "log_level": "INFO",
32            "kl_coeff": 1.0,
33            "num_gpus": 0,
34            "horizon": 1600,
35            "observation_filter": "MeanStdFilter",
36            "model": {
37                "fcnet_hiddens": [32,32],
38                "free_log_std": True
39            },
40            "num_sgd_iter": 10,
41            "sgd_minibatch_size": 128,
42            "lambda": sample_from(lambda spec: random.uniform(0.9, 1.0)),
43            "clip_param": sample_from(lambda spec: random.uniform(0.1, 0.5)),
44            "lr": sample_from(lambda spec: random.uniform(1e-3, 1e-5)),
45            "train_batch_size": sample_from(
46                lambda spec: random.randint(1000, 60000))
47        })

LinkFuture work

This approach opens the door to several exciting future directions, which we hope will be enabled with the new open source code. For example, is it possible to go beyond continuous hyperparameters and use probabilistic models to learn architectures or even algorithms? We can also consider ways to make it more efficient using off policy data. Finally, we could try to adapt the population size online, rather than keeping it fixed throughout training. 

LinkSummary

PB2 provides a promising approach for efficient hyperparameter tuning, combining the best of Population Based Training with Bayesian Optimization. 

It is included as a new algorithm in Ray Tune, and you can check out the full code example here! Or you can try out PB2 to optimize the hyperparameters for your own model or reinforcement learning task, and even use Ray’s cluster launcher to run multi-node experiments on the cloud. 

Please do not hesitate to get in touch for all follow up questions on the paper or the code! And if you would like to try out any of the other algorithms or features from Tune, we’d love to hear from you either on our Ray Discourse or Slack!