Scaling up PyTorch Lightning hyperparameter tuning with Ray Tune

PyTorch Lightning has been touted as the best thing in machine learning since sliced bread. Researchers love it because it reduces boilerplate and structures your code for scalability. It comes fully packed with awesome features that enhance machine learning research.

Here is a great introduction outlining the benefits of PyTorch Lightning.

But with any machine learning workflow, you’ll need to do hyperparameter tuning. The right combination of neural network layer sizes, training batch sizes, and optimizer learning rates can dramatically boost the accuracy of your model. This process is also called model selection.

Join us for Ray Summit online! Keynotes and sessions, Sept 30-Oct 1 (free!). Tutorials, Sept 29.

In this blog post, we’ll demonstrate how to use Ray Tune, an industry standard for hyperparameter tuning, with PyTorch Lightning. Ray Tune provides users with the ability to 1) use popular hyperparameter tuning algorithms, 2) run these at any scale, e.g. single nodes or huge clusters, and 3) analyze the results with hyperparameter analysis tools.

By the end of this blog post, you will be able to make your PyTorch Lightning models configurable, define a parameter search space, and finally run Ray Tune to find the best combination of hyperparameters for your model.

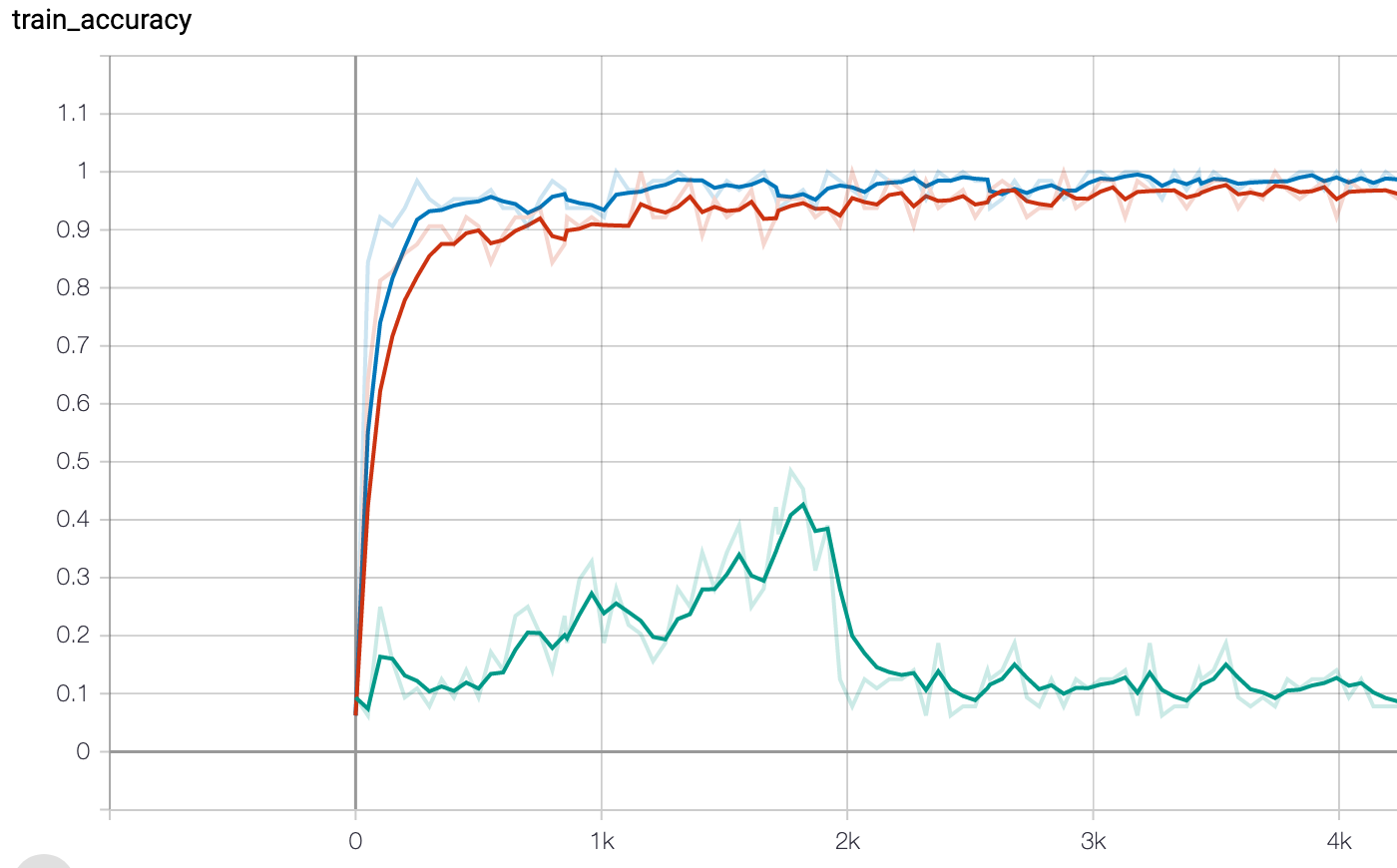Hyperparameter tuning can make the difference between a good training run and a failing one. This is the same model, trained with three different sets of parameters.

LinkInstalling Ray

Tune is part of Ray, an advanced framework for distributed computing. It is available as a PyPI package and can be installed like this:

1
pip install "ray[tune]" pytorch-lightning

LinkSetting up the LightningModule

To use Ray Tune with PyTorch Lightning, we only need to add a few lines of code. Best of all, we usually do not need to change anything in the LightningModule! Instead, we rely on a Callback to communicate with Ray Tune.

There are only two prerequisites we need. First, your LightningModule should take a configuration dict as a parameter on initialization. This dict should then set the model parameters you want to tune. This could look like this:

1
2
3
4
5
6
def __init__(self, config):
  super(LightningMNISTClassifier, self).__init__()
  self.layer_1_size = config["layer_1_size"]
  self.layer_2_size = config["layer_2_size"]
  self.lr = config["lr"]
  self.batch_size = config["batch_size"]

(Click here to see the code for the full LightningModule)

Second, your LightningModule should have a validation loop defined. In practice, this means that you defined a validation_step() and validation_epoch_end() method in your LightningModule.

LinkTalking to Tune

Now we can add our callback to communicate with Ray Tune. The callback is very simple:

1
2
3
4
5
class TuneReportCallback(Callback):
  def on_validation_end(self, trainer, pl_module):
    tune.report(
      loss=trainer.callback_metrics["val_loss"].cpu(),
mean_accuracy=trainer.callback_metrics["val_accuracy"].cpu())

This means that after each validation epoch, we report the loss metrics back to Ray Tune. The trainer.callback_metrics dict is automatically populated by PyTorch Lightning. The val_loss and val_accuracy keys correspond to the return value of the validation_epoch_end method. We make also make sure the metrics are available on the CPU for Ray Tune to work with.

Ray Tune will start a number of different training runs. We thus need to wrap the trainer call in a function:

1
2
3
4
5
6
7
8
def train_tune(config, epochs=10, gpus=0):
  model = LightningMNISTClassifier(config)
  trainer = pl.Trainer(
    max_epochs=epochs,
    gpus=gpus,
    progress_bar_refresh_rate=0,
    callbacks=[TuneReportCallback()])
  trainer.fit(model)

The train_tune() function expects a config dict, which it then passes to the LightningModule. This config dict is populated by Ray Tune’s search algorithm.

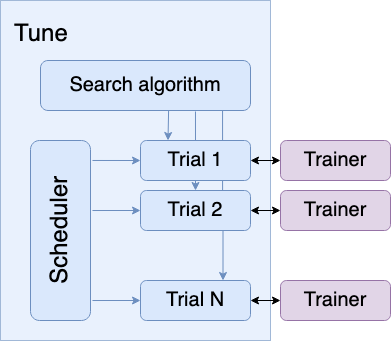Ray Tune’s search algorithm selects a number of hyperparameter combinations. The scheduler then starts the trials, each creating their own PyTorch Lightning Trainer instance. The scheduler can also stop bad performing trials early to save resources.

LinkDefining the search space

We now need to tell Ray Tune which values are valid choices for the parameters. This is called the search space, and we can define it like so:

1
2
3
4
5
6
config = {
  "layer_1_size": tune.choice([32, 64, 128]),
  "layer_2_size": tune.choice([64, 128, 256]),
  "lr": tune.loguniform(1e-4, 1e-1),
  "batch_size": tune.choice([32, 64, 128])
}

Let’s take a quick look at the search space. For the first and second layer sizes, we let Ray Tune choose between three different fixed values. The learning rate is sampled between 0.0001 and 0.1. For the batch size, also a choice of three fixed values is given. Of course, there are many other (even custom) methods available for defining the search space.

LinkRunning Tune

Ray Tune will now proceed to sample ten different parameter combinations randomly, train them, and compare their performance afterwards.

We wrap the train_tune function in functools.partial to pass constants like the maximum number of epochs to train each model and the number of GPUs available for each trial. Ray Tune supports fractional GPUs, so something like gpus=0.25 is totally valid as long as the model still fits on the GPU memory.

1
2
3
4
5
from functools import partial
tune.run(
  partial(train_tune, epochs=10, gpus=0),
  config=config,
  num_samples=10)

The result could look like this:/media/9a1ef78a06b7e19f8b97d19e4bea8c4e

In this simple example a number of configurations reached a good accuracy. The best result we observed was a validation accuracy of 0.978105 with a batch size of 32, layer sizes of 128 and 64, and a small learning rate around 0.001. We can also see that the learning rate seems to be the main factor influencing performance — if it is too large, the runs fail to reach a good accuracy.

LinkInspecting the training in TensorBoard

Ray Tune automatically exports metrics to the Result logdir (you can find this above the output table). This can be loaded into TensorBoard to visualize the training progress.

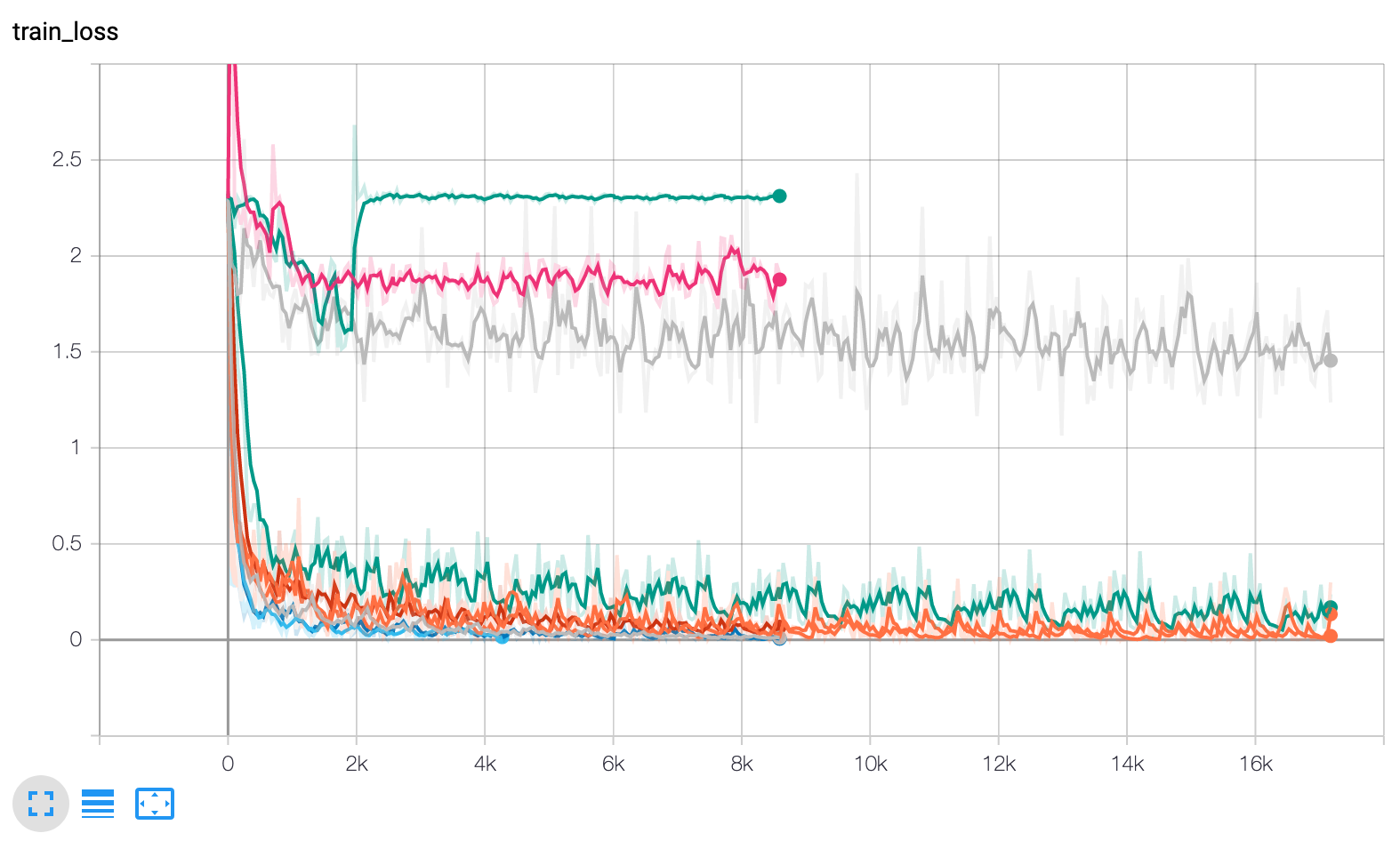
LinkConclusion

That’s it! To enable easy hyperparameter tuning with Ray Tune, we only needed to add a callback, wrap the train function, and then start Tune.

Of course, this is a very simple example that doesn’t leverage many of Ray Tune’s search features, like early stopping of bad performing trials or population based training. If you would like to see a full example for these, please have a look at our full PyTorch Lightning tutorial.

Parameter tuning is an important part of model development. Ray Tune makes it very easy to leverage this for your PyTorch Lightning projects. If you’ve been successful in using PyTorch Lightning with Ray Tune, or if you need help with anything, please reach out by joining our Ray Discourse or Slack — we would love to hear from you.

Join us for Ray Summit online! Keynotes and sessions, Sept 30-Oct 1 (free!). Tutorials, Sept 29.